Record some of my challenge-solving ideas for Securinets CTF 2022,if there are any discrepancies ,plz correct me ~.

Sherry

task.py:

#!/usr/bin/env sage
from sage.all import *
from Crypto.Util.number import *
import random, sys, json

FLAG = "Securinets{REDACTED}"

def getRandomElement(F, deg):
        return F.random_element(degree=deg)

def polyToList(p):
        return p.list()

def listToPoly(F, l):
        return sum(F(c*x**i) for i, c in enumerate(l))

def polySum(p1, p2):
        if p1.parent() == p2.parent():
                return p1 + p2
        else:
                return p1 + p1.parent()(p2)

def getShare(g, secret):
        y = g**secret
        print(polyToList(y))
        e = getRandomElement(PolynomialRing(GF(getPrime(256)), "x"), 10)
        print(e)
        s = polySum(y, e)
        share = polyToList(s)
        return share


if __name__ == '__main__':
        print(f"Welcome to Black Organization.\nTo join us, you have to guess our secret.\n")

        p = getStrongPrime(512)
        P = PolynomialRing(GF(p), "x")
        x = P.gen()
        N = getRandomElement(P, 10)
        Q = P.quotient_ring(N**2)
        x = Q.gen()

        G = Q(getRandomElement(P, 10))
        secret = random.randint(1, p-1)
        print(secret)
        pub = G**secret

        params = {"N": polyToList(N), "pub": polyToList(pub), "G": polyToList(G), "p":p}
        print(f"{params}\n")

        for _ in range(5):
                try:
                        g = eval(input("Your guess g : "))
                        s = eval(input("Your guess s : "))

                        g = listToPoly(Q, g)
                        s = int(s, 16) % p

                        if g**s == pub:
                                if s != secret:
                                        print(f"Don't cheat! :)")
                                        continue
                                print(f'From now, your name will be Sherry! Here is your flag : {FLAG}')
                                sys.exit()

                        else:
                                share = {'share': getShare(g, secret)}
                                print(f'{share}\n')

                except Exception as e:
                        print(e)
                        sys.exit()

根据 题意 分析，我们可以得到以下关系。

其中g是我们发送给服务器方的一个参数，G,N,share以及他们是在GF(p)下的，并且p是512位，而y1以及e1我们不知道，而其中e1是256位的一个11个系数 度为10的多项式。

这道题是需要我们找到secret，并且满足

我们如果给出g,s不符合 g^s == pub ，则服务器返回一个share就是上述的share。

到这里我们或许会尝试 g = pub ,s = 1，但是很不幸，”Don’t cheat! :)”。

接下去我们可以发现如果给出g=a（a是一个常数），大致是可以通过HNP的手段将a ^ secret % p恢复出来，可是这里就出现问题了，我恢复出来了a ^ secret % p，但是p是一个strongPrime,那么我们没有办法求得他的阶，很遗憾，Failed。

再想想，如果secret是一个奇数，我给出g=N+1，他返回的是

但是N的度和e的度是10，怎么样才能把它们区分开来，第一个想到的是将值%N，但是发现得到的值可能会比较大，但是这里我们可以发现

这样我们接下去对他进行LLL一下，构造格子

LLL之后拿到只要e的大小接近256bit，那么就是对应得到的secret了。

接着回代即可。

AES^2^

task.py:

from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
import os, sys, hashlib, random

FLAG = b"Securinets{REDACTED}"

key, iv1, iv2 = [os.urandom(16) for _ in range(3)]

def xor(a, b):
	return bytes(i ^ j for i, j in zip(a, b))

def get_token(msg, iv1, iv2):
	if len(msg) % 16 != 0:
		msg = pad(msg, 16)
	aes = AES.new(key, AES.MODE_ECB)
	blocks = [msg[i:i+16] for i in range(0, len(msg), 16)]
	enc = b""
	tmp1 = iv1
	tmp2 = iv2
	for block in blocks:
		tmp = aes.encrypt(xor(block, tmp1))
		_tmp = aes.encrypt(xor(tmp, tmp2))
		enc += _tmp
		tmp1 = _tmp
		tmp2 = tmp
	return enc

def proof(msg):
	res = b"\x00"*16
	for i in range(0, len(msg), 16):
		res = xor(res, msg[i:i+16])
	return hashlib.sha256(res).digest()


if __name__ == "__main__":
	alice_username = os.urandom(32)
	alice_token = get_token(alice_username, iv1, iv2)
	print(f"Alice's creds : {alice_username.hex()} -> {alice_token.hex()}\n")

	while True:
		try:
			username = bytes.fromhex(input("Username : "))
			token = get_token(username, iv1, iv2)
			print(f"Your creds : {username.hex()} -> {token.hex()}")

			if proof(token) == proof(alice_token):
				if token == alice_token:
					print(f"You are not Alice!")
					sys.exit()
				else:
					print(f"Hey Alice! Here is your flag {FLAG}")
					sys.exit()	
			else:
				print("Try again!\n")
		except Exception as e:
			print(e)
			print("Invalid input.\n")

分析题目中需要得到proof(Aliceusername) == proof(myusername)，而这里他proof部分使用的是xor，其中我们可以想到如果是有长度限制的话很容易想到去交换enc1和enc2的位置去得到，但是目前我认为并没有办法做下去。

但是该题没有长度限制，我们想它既然是xor，的那么我只需要让后面加2块(maybe more?)去使得他能够得到的enc3^enc4=0即可。

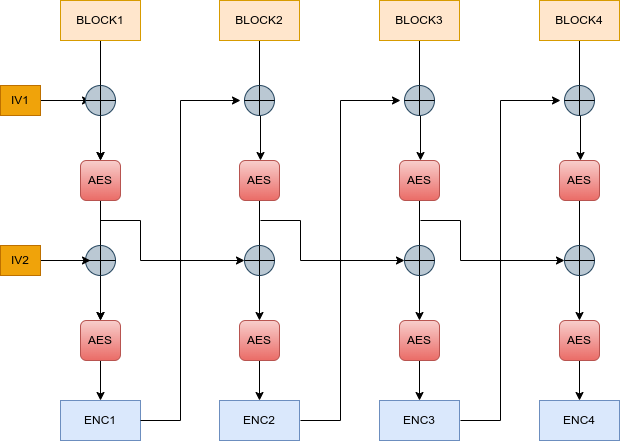
在这里我们可以发现BLOCK和ENC是可控的，即可以做到CPA。

在第二块以后的IV1部分我们也是可以控制其第一次AES之前的值，但是AES之后我们就不可知，只有ENC2之后是可知的。

2次AES之间存在一个XOR IV2，我们可以发现他与这块使用的IV2无关，只与上一块前半部分AES有关，那么可以控制后面只需要使得ENC3和ENC4相等即可，往回推，如果可以使得BLOCK2和BLOCK3第一次AES后相同即可，而这里我们发现他AES之前使用的异或值我们都是可知的，那么ENC1 ^ BLOCK2=ENC2 ^ BLOCK3即可做到在ENC3和ENC4部分对于前一次AES用于异或的值相同。那么接下来只需要第一次AES前输入的值相同即可得到ENC3==ENC4，与第二块和第二块相同分析，使得ENC3 ^ BLOCK4 = ENC2 ^ BLOCK3 = ENC1 ^ BLOCK2

:=> BLOCK3 = ENC1 ^ BLOCK2 ^ ENC2 ; BLOCK4 = ENC1 ^ BLOCK2 ^ ENC3 ;

这样就可以做到成功伪造。

Well

只要跟着题目的流程走即可得到同构下的key是相同的。