这周末看的Neobeo出的一道题,但是没做出来,有限域上的知识差太远了。跟着writeups复现了一遍,但是还有点不是很清楚的地方,回头再来补一下这点内容。
description 1 2 3 4 5 6 By Neobeo I wrote a hash function in under ten lines! It uses finite fields to prevent any leakage of the flag. Hint: Use the first 20 coefficients of x^2286 and x^2304 (plus the known 20 bytes of the flag), to solve the remaining 9 bytes as a linear system.
题目附件如下:
1 2 3 4 5 6 7 8 import stringflag = open ('flag.txt' ).read().strip().encode() F = GF(127 ^29 , 'x' , modulus=list (flag)) FlagHash = lambda s: bytes ((F(list (s.encode()))^128 ).polynomial()[:20 ]).hex () for _ in range (1337 ): s = '' .join(sample(string.ascii_letters + string.digits, randint(13 ,37 ))) print (s, FlagHash(s))
随机生成13-37长度的明文,并且计算出他的FlagHash
Analysis 看到题目一开始,感觉很神奇,把他直接转换成稍微复杂点,好理解的代码,如下
1 2 3 4 5 6 7 8 9 10 11 import stringflag = b'vsctf{Fake_Flag_with_Padding_}' PR.<x> = PolynomialRing(GF(127 ^29 )) Q = PR.quo(PR(list (flag))) x = Q.gens()[0 ] def FlagHash (s ): tmp = list (Q(list (s.encode()))^128 )[:20 ] rec = "" for _ in range (len (tmp)): rec+=hex (int (tmp[_]))[2 :].rjust(2 ,"0" ) return rec
由于他截断了,因此得到
如果是没有截断的直接最后GCD即可,代码如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 import stringflag = b'vsctf{Fake_Flag_with_Padding_}' PR.<x> = PolynomialRing(GF(127 )) Q = PR.quo(PR(list (flag))) x = Q.gens()[0 ] def FlagHash (s ): tmp = list (Q(list (s.encode()))^128 ) rec = "" for _ in range (len (tmp)): rec+=hex (int (tmp[_]))[2 :].rjust(2 ,"0" ) return rec def trans (msg ): return PR(list (bytes .fromhex(msg))) fs = {} for _ in range (4 ): s = '' .join(sample(string.ascii_letters + string.digits, randint(13 ,37 ))) print (s, FlagHash(s)) fs[s] = FlagHash(s) tmp = PR(list (s.encode()))^128 - trans(FlagHash(s)) for s in fs.keys(): tmp = gcd(tmp,PR(list (s.encode()))^128 -trans(FlagHash(s))) list (tmp*125 ) == list (flag)
在比赛过程中,并没有求解出来这道题,Hint也没有用上,于是赛后根据 Author’s write-up for FlagHash - HedgeDoc 进行学习复现…
Part 1: Recovering the forward map 这里涉及到一个映射 field theory - Frobenius Automorphism as a linear map - Mathematics Stack Exchange 给出了一个理论
Let We can view In this case,
本题中给出的p=127,n=29,那么当
那么原映射
由此我们可以得到
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Ms = [] for _ in range (1 ): F = PolynomialRing(GF(127 ),29 *29 ,'x' ) xs = F.gens() Mtmp = Matrix(F,29 ,29 ,xs) s_mat = [] v_tar = [] coefs = [] for i in trange(29 *29 ): s_mat = vector(F,vs[i][0 ]) ti = s_mat*Mtmp*s_mat coef = [0 for _ in range (29 *29 )] for __ in ti.variables(): coef[xs.index(__)] = ti.coefficient(__) coefs.append(coef) v_tar.append(vs[i][1 ][_]) coefs_ = Matrix(GF(127 ),29 *29 ,29 *29 ,coefs) targe_ = Matrix(GF(127 ),29 *29 , 1 ,v_tar) M_ = coefs_.solve_right(targe_) Ms.append(M_)
出题人的脚本又快又简洁….tnbl
1 2 mat = matrix(GF(127 ), [[x*y for x in v_in for y in v_in] + v_out for v_in, v_out in vs]) soln = mat[:,:841 ].solve_right(mat[:,841 :])
这些矩阵可以完全确定映射,因此现在可以对想要的任何字符串进行哈希处理(只要它不超过 29 个字符)。
Part 2: Recovering first 20 bytes of flag 我们发现前五行如下
1 2 3 4 5 6 sage: soln[:5 ] [ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] [ 37 89 83 121 2 50 93 14 75 68 108 32 52 58 53 30 65 102 103 33 ] [108 3 88 52 51 88 10 118 109 106 37 94 55 88 54 74 24 85 39 54 ] [ 1 66 18 100 90 102 44 116 57 23 9 4 56 73 6 31 31 87 74 6 ] [ 14 59 74 30 121 50 0 20 45 11 37 47 31 96 99 124 32 63 18 54 ]
下面是我的代码跑的,M1就是第一列的841个参数的前5个,可以check一下
1 2 3 4 5 6 sage:M_[0 :5 ] [ 1 ] [ 37 ] [108 ] [ 1 ] [ 14 ]
这些行对应于多项式(的前 20 个系数):
事实上,对于任意的
这是咋推出来的(好奇.jpg,因为x^p+x是kernel吗?)
感谢来自utaha的解答 其中可以发现这个Frobenius Automorphism满足在GF(127)情况下满足
那么很容易就可以得到
可以通过第二条计算x^127%flag的前20个的值;当
1 2 3 4 x127 = soln[1 ] - vector([i==1 for i in range (20 )]) x128 = soln[30 ]
其中
1 2 3 4 first20 = x128 - vector([0 ]+list (x127)[:-1 ]) first20 *= ord ('v' ) / first20[0 ] first20 = bytes (first20)
由于位移,我们可以通过
1 -mod(66 ,127 ) * ord ('}' ) / ord ('v' )
来计算出最后一位的时候移了多少,直接用Neobeo的图来看,这个用在第三步中
Part 3: Recovering the last 9 bytes 现在剩下九个byte需要去恢复。需要了解上面和下面的内容才能从中获得一些信息,或者通过转换,我们可以将一个系数与其右下角的系数联系起来。
在这种情况下,我们实际上可以通过 19 个连续的幂来弥补这9个的差距。Neobeo是使用
1 2 3 4 x2286 = soln[18 ] - vector([i==18 for i in range (20 )]) x2304 = soln[30 *18 ]
也直接借用Neobeo的图来看看他的这个模数移位
2286-2304之间的值主要是根据前面提到的多项式
References [1] : Author’s write-up for FlagHash - HedgeDoc
[2] : field theory - Frobenius Automorphism as a linear map - Mathematics Stack Exchange

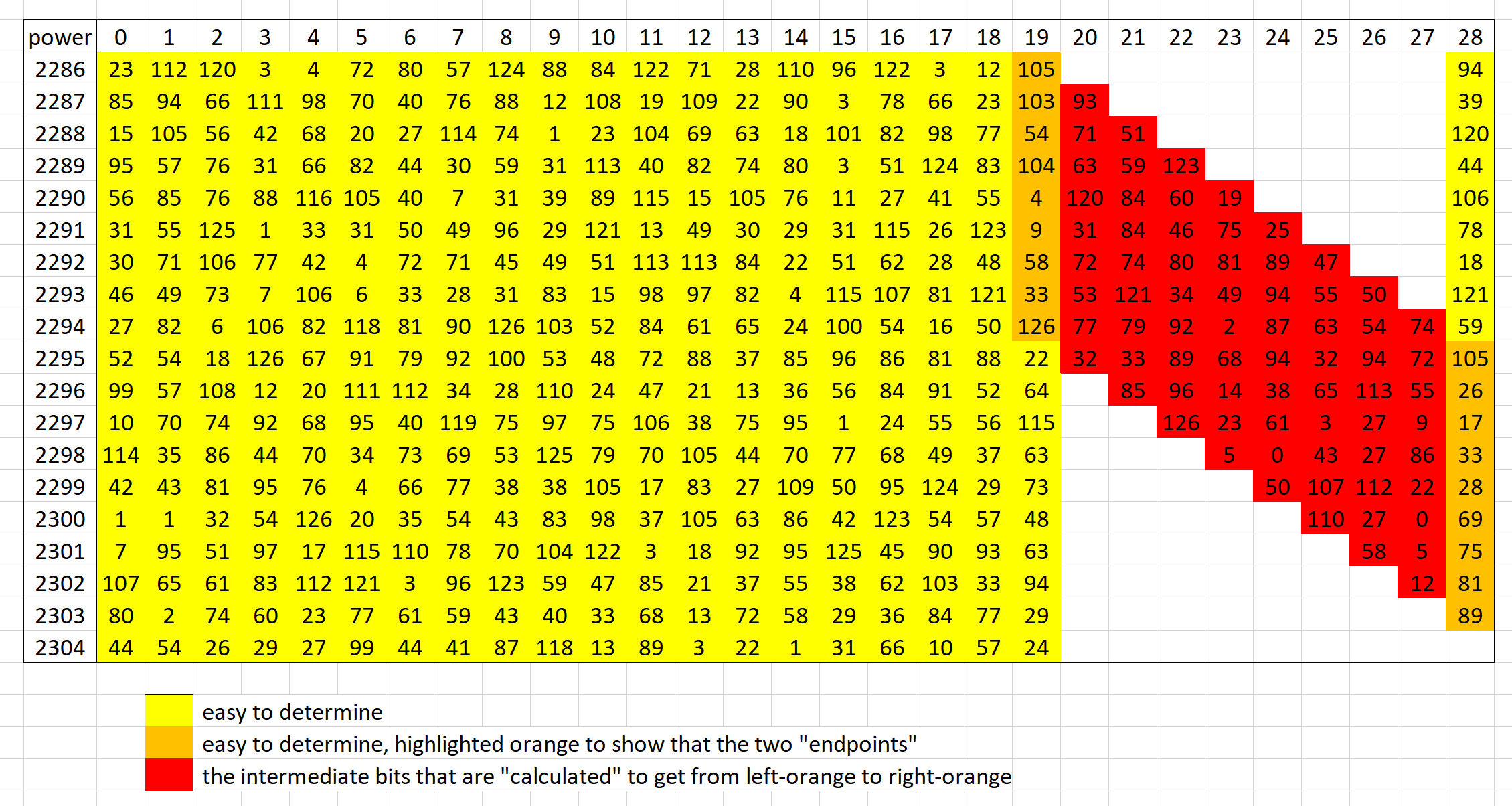 长度为 9 的间隙代表模数的未知部分,但通过这种方式将它们链接起来,发现它实际上只是一个线性方程组。(不需要求解所有中间红色值,这个图用于演示)
长度为 9 的间隙代表模数的未知部分,但通过这种方式将它们链接起来,发现它实际上只是一个线性方程组。(不需要求解所有中间红色值,这个图用于演示)